江戸時代に興った庶民の数学「和算」やその研究成果を絵馬に記して寺社仏閣に奉納した「算額」にロマンを感じ、 その内容をネタに当時の日本人が持っていた数学的発想や思考様式をじっくり追って行こうというのがこの頁の趣旨です。 現代の日本人が数学的思考をするとき、当時の和算的発想は少なからずその遺伝子なり潜在意識に影響を及ぼしているも のと思われます。この意味でもこの企てはそれなりの価値を持つでありましょう。その名も「山岳会」をぱくっています が、皆さん広大な数学の荒野で遭難しないよう各自気を付けましょう。
(画像をクリックすると拡大できます)
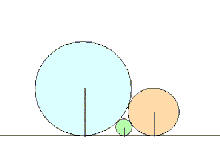[1]最初によく知られた塁円術の基本的な問題です。奈良・興福寺に掲げられていた算額に記された第一問題だそうで、図の
ように大円と中円に接する小円の半径 c を問うています。大中円の半径 a, b は既知とします。「術」とよばれる解法は各二
円の中心を結んで三平方の定理により:
abの平法根 = bcの平法根 + caの平法根 の関係を得て答えを導きます(あ
あ数学ソフトが欲しい!)。
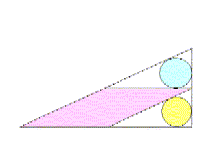[2]ちょっと悩んだ第二問です。上下の円の直径が各々13と12のとき左の菱形の一辺の長さを求める問題です。まず直角三角形の相似比
により、よく知られた13:12:5の直角三角形であることが判ります。この場合簡単な計算により内接円の直径対底辺の比が1:3であ
ることが判り、菱形の辺をなす上の三角形の底辺が13 x 3で39を得ます。この問題は山口和が文化十五年(1818年)仙台方面で
見付けた算額に記されていたそうです。
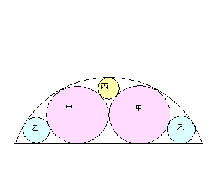[3]まだ解けない第三問です。弓形の中に直径が72寸の甲円が２個と直径が32寸の乙円が２個入っている。ここに丙円１個を加えると
その直径はいくらになるか、という問題です。まず大円の半径や弓形の「矢」つまり高さを求めることが必要と思われるのです
が、手掛かりが掴めません。算額問題には不完全なものや、間違っていてそもそも解けないものもあるそうですが、この場合はど
うなんでしょう? この算額は播磨の国は書写山円教寺の観音堂に掛かってたもので、文政四年(1821年)に澤珠介正敬という人が奉
納しました。山口和はこの人と会って算額に記された諸問題について話をしているので、多分解ける問題なのでしょう。
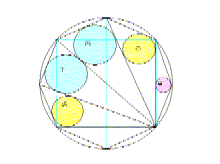[4]ご存知信濃の国は善光寺に掛かっていた算額の問題です。例えば一辺が a の正八角形の一頂点から対角線を順次引き、できた三角形
に内接円を入れていきその直径を求めるというものです。文化元年六月に関五太夫が奉納したものです。善光寺は何度も訪れてい
るのでひょっとすると宝物殿などでお目に掛かっていたかも知れません。術としては正八角形を容れる大円の半径 r が a / (2 - 2
の平方根)の平方根 で得られるのでこれを使って、直角三角形に内接する丙円の径は直ちに得られ、甲円と乙円の径も一旦上半の直角
三角形に内接する円の径を求めて、相似形の比例計算により対角線を底辺とする三角形の内接円の径を求めることができます・・・・
と思って検証してみたら、乙円を求める相似比例関係が旨く把握できません。助けて下せぇ、お大師様 !
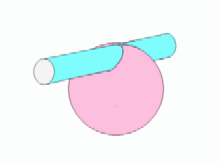[5]これは日経サイエンスのHPに掲載されている問題の写しですが、図のように球面を円柱面が貫通しています。両者は球の頂点で一点
で交わっています。球面に囲まれた部分の円柱面の面積を求めます。頂点から垂らした軸に沿った距離を積分変数として、これに対
応する面積の増加分を積分して案外すっきりと解決しています。最初問題を見たときは、よくこんなややこしい積分問題が和算で解
けたものだと驚嘆を禁じ得ませんでした。描画能力上ここでは詳しく説明できませんので当該HPを参照して下さい(解の式中に二箇所
タイプミスがありますがほぼ自明なものです)。
[6]これは関孝和の名とならんで教科書などでよく紹介される代表的な塁円術の問題ですね。図中に繰り返して現れる黄と青の円の大きさ
を緑の大円を基準にして求めるというものです。ピタゴラスの定理を繰り返し用いても順次解いていけるのですが、上述の日経サイ
エンスのHPでは双曲幾何の円に関する反射定理を用いて無限縮小円列を等円の無限列に反射して、そこからｎ番目の円の大きさを
求める公式を導いています(ここにもタイプミス数箇所有)。この問題に双曲幾何を用いたことは正に目からウロコの発想です。
[中締]ここまで調べてきて感じることですが、算額って江戸時代のビジュアルアートでもあったのですね。
そのモチーフは正に鮮やかに彩色された幾何学模様そのものです。美術的レベルに劣らず内容も高度なものが多いようですが、目に
付くのは平面幾何にせよ立体幾何にせよ構造が内向きでその多くに繰り返しが見られることです。具体的には初めに大きな入れ物と
して大円なり円筒なりの図形があり、その中に内接円や内接球等を嵌め込んでいくという内向き構造、内向的フラクタルとでも言う
か、そしてそれが現代の不動点定理にまで繋がるのでしょうか。昔から日本人が内向的なＡ型民族で、それが数学好きにも表れて
いたということでしょうか・・・
算額会も徐々に佳境に入ってきました。寺小屋で九九や八算を暗唱する利発な子供たちの声が聞こえてきませんか・・・ニイチテンサ
クノゴ、ニシンガイチジュウ、サンイチサンジュウイチ・・・
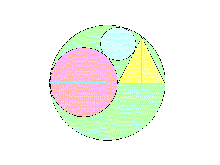[7]1803年群馬県で奉納された算額の問題です。大円の直径上に、互いに接する中円と二等辺三角形が各々その中
心と底辺を載せて大円に内接しています。大円に内接し、中円と二等辺三角形に外接する新たな円を描くとその中心が、中円と三角
形の接点で大円の直径と直交する直線上にあることを証明するものです。これも日経サイエンスのHPで見付けたもので、解答はそち
らに譲ります。見掛けは極単純そうですが、三平方の定理と三角関数を用い精密な代数計算を駆使してようやく証明を得ています。
こうして眺めると算額問題の構造は、その緻密さには時として凄みすら感じられますが、箱庭的な狭さ窮屈さに支配されているよう
な印象を受けるのは独り私のみでしょうか・・・?
[8]箱庭的と言ったら本当に四角い枠に収まった問題がありました。1874年群馬県で奉納された算額の問題だそう
で、これまた日経サイエンスのHPからの写しです。これは中学か高校で習ったような気がする「ケージーの定理」とやらを使って、
４個の黄色い円の半径と正方形の一辺との関係を求めるものです。まだケージー(Casey)の定理自体正確に理解していませんが、当
該HPによる関係式を正方形の一辺 a の二次方程式に関して解いてみました。かなりな量の計算を経て得られた結果は、そこに提示
されているものとは少し違っていました。分母が全４半径の和となり、また分子のルートの中が係数の２以外が異なりました。ここで
得られるもうひとつの結論・・・和算家は非常に根気強かった!
(１０日ほど経過)で、「日本の数学--何題解けますか?[下](森北出版)」を買ってケージーの定理を理解し、出だしの式まで納得が
行きました。しかしここからの計算は煩雑としてこの書籍の解答編でも端折ってあるではないですか・・・! いずれ暇を見付けても
う一度検証してみましょう。
(それから一月ほど経過)で、夏の夜中に落ち着いて計算を何度もやり直した結果、分母は日経サイエンスのHPにある通りr1-r2+r3-r4
が正当となりました。しかし分子のルートの中だけは未だに提示されているものとは食い違ったものが得られています・・・!?
組織: 個人商店「鉄道カフェ・門トス」
所在地: 〒841-0032佐賀県鳥栖市大正町784-7-3F
代表: 田中伍夫(たなかいつお)
メールアドレス: rinkoh@hid.bbiq.jp
電話&FAX: 0942-80-2332